5ドル!ラズパイ・ゼロ(Raspberry pi Zero)でIoT (22) アナログ温度センサ4 サーミスタ
■適材適所!コストダウンに寄与する温度センサ
サーミスタは、温度が上がると抵抗値が減少する特性をもった抵抗です。利用するのはNTC(Negative Temperature Coefficient thermister)タイプで、温度と抵抗値の関係はほぼ比例していますが、線形ではありません。
利用することの多い-20℃付近から100℃付近では、抵抗をつなぐだけの簡単な回路で大きな電圧変化が得られるので、微小な出力のセンサより扱いやすいのが特徴です。精度の良い温度測定より、設定した温度を超えると何かアラートを出力するような用途に向いているので、産業用では多く使われています。
●そんなに非線形なのか
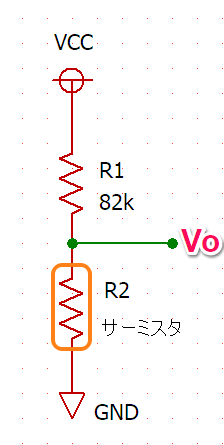
温度と電圧が比例関係にあると計算しやすいので、回路も短時間に決定できます。入手したNXFT15XH103FA 10kΩを下記の回路で測定しました。執筆時点の価格は40円です。
一度ヒート・ガンで高温にして、温度が下がっていくときに記録しました。温度は、おんどとりTR-7nwを使って測りました。被試験サーミスタとおんどとりの温度センサであるサーミスタをテープで巻き、プチプチでくるみました。
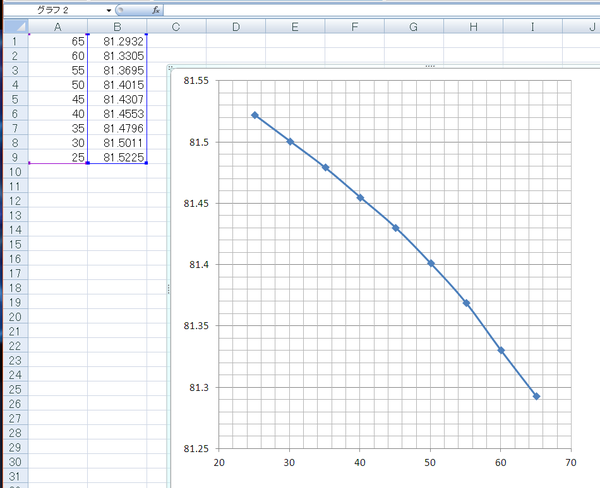
直列に入った抵抗そのものにも温度係数があります。抵抗温度係数TCR(Temperature Coefficient of Resistance)は、抵抗値の変化を1℃あたりの百万分率で表したものです。金属皮膜抵抗は抵抗メーカの資料によると±5~±200、炭素皮膜抵抗はそれよりも数倍大きいです。実際に82kΩの金属皮膜抵抗を測りました。25~65℃の範囲で-70×10^-6/Kとなり、前出の値と異なりますが、大きくありません。
25℃から65℃では 抵抗値の変化は0.4%と小さいので無視できます。
下記の回路で出力電圧Voの温度依存性を測定しました。電源電圧Vccは測定中5.01919~5.01889Vの間で変動しましたが、これも変化が少ないので、無視します。
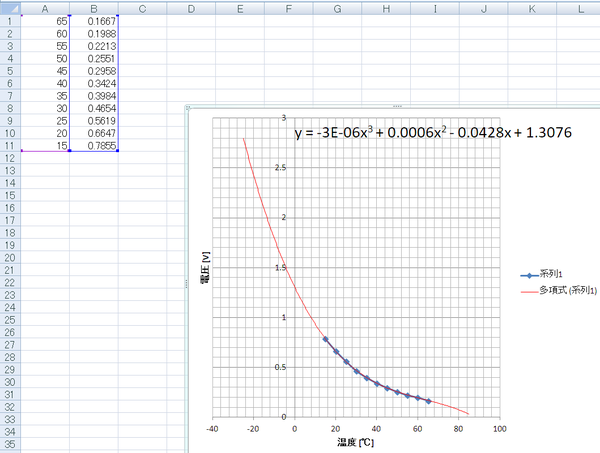
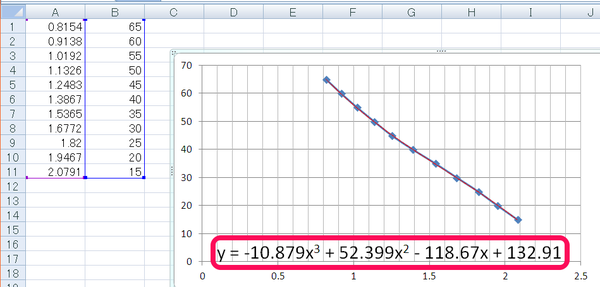
エクセルに測定したデータを入れ、3次曲線で低温側と高温側を予測しました。
- -20℃付近まで測定するときは、A-D変換の基準電圧は3.3V付近が適している
- 常温付近を測りたいときは、基準電圧は1.0Vが適している
- 常温より高い温度を測りたいときは、直列に入っている抵抗を変更する
●A-Dコンバータは10ビットを使う
サーミスタが低価格な温度センサなので、コストを抑えるためにA-Dコンバータも10ビットを使います。組み込み用マイコンでは10ビットのA-Dコンバータが内蔵されていることも多いです。
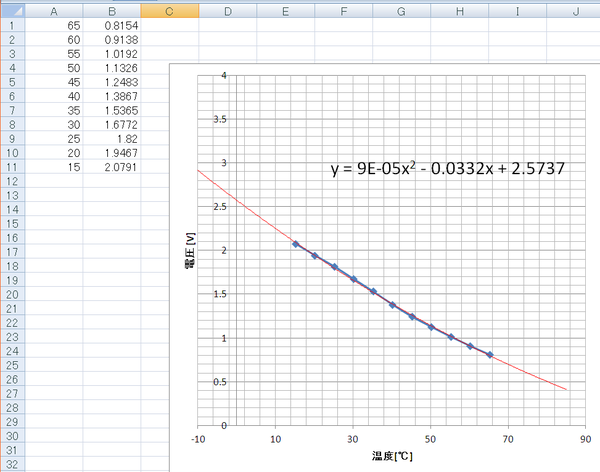
部品点数を少なくしてコストを下げるために基準電源に3.3Vの電源を使うと、常温付近のデータが粗いです。上記の実験で使った82kΩを8.2kΩに変更して、データを取り直しました。
接続方法は、下記のページと同じです。
5ドル!ラズパイ・ゼロ(Raspberry pi Zero)でIoT (9) A-Dコンバータの利用6 MCP3002/MCP3008
電源電圧は3.29566Vです。エクセルの予測では-10℃から90℃付近まで、大きく電圧が変化します。10ビットA-Dコンバータは、分解能は粗いです。
|
3.29566 / 2^10 = 3.22 mV |
計算式から25℃と25.1℃の電圧差は2.87mVです。したがって、10ビットA-Dコンバータでは0.1℃の分解能はとれませんが、それに近いデータが取れることがわかります。
●プログラム
温度と電圧の軸を入れ替えて、電圧から温度が導けるようにグラフを変更し、変換式を得ます。
#!/usr/bin/env python
from gpiozero import MCP3002
Vref = 3.29566
while 1:
pot = MCP3002(channel=0)
Volt = pot.value * Vref
Temp = -10.879 *Volt*Volt*Volt + 52.399*Volt*Volt - 118.67*Volt +132.91
print Volt,"V ",round(Temp,1),"C"
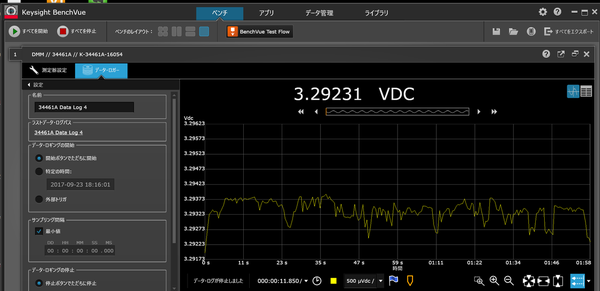
常に変動する電源を基準電圧Vrefとして利用したので、10回分測定した平均を取ればより安定な温度が取得できます。次の図は、ラズパイの電源電圧のロギング例です。
ここまでで使ってきた温度センサの中で、温度変化にすばやく対応するデバイスの一つです。
●B定数を使う
データシートには25-50℃のB定数は3380と書かれています。この数値を使って温度を計算します。
測定した電圧Voからサーミスタの抵抗Rを求めるには、電源電圧をVrefとするとRと8.2kで分圧されているので、
| Vo = Vref * ( R/R+8.2k ) R = -(8.2k*Vo)/(Vo-Vref) |
Vref=3.3V、Voが半分の1.65Vとすると、サーミスタの抵抗値は8.2kΩと同じになります。
R=-(8.2k*1.65)/(1.65-3.3) = -(8.2k*1.65)/-1.65=8.2k
B定数の式です。
| R = Ro * exp(B*( 1/(T+273.15) - 1/(To+273.15) )) |
温度Tについて変形します。
| T =1/(1/(To+273.15)+ln(R/Ro)/B)-273.15 |
Ro=10k (基準温度時の抵抗値)、To=25℃(基準温度) 、B=3380とすると、
T=1/(1/(25+273.15)+ln(R/10k)/3380)-273.15
ここで、サーミスタの抵抗値R=8.2kのときの温度は次のように計算できます。実測のグラフから読み取った値とほぼ同じです。
T=30.3℃
Rに測定電圧Voを代入します。
| T =1/(1/(To+273.15)+ln( (((-8.2k*Vo)/(Vo-Vref) )/Ro)) /B) - 273.15 |
測定したVo=1.7V 、Vref=3.3V、Ro=10k 、To=25℃ 、B=3380とすると、温度(摂氏)が求まります。
T =1/(1/(25+273.15)+ln( (((-8.2k*1.7)/(1.7-3.3) )/10000 )) /3380 ) -273.15
=28.6℃
(※ 2018/06/07訂正) T=の式中、Roの後ろにあったパーレンを一つから二つにした。下のプログラムは正しい。
プログラムは、次のように2通りの方法で求めた温度を併記しました。二つの温度差も表示しました。8.2kΩの抵抗は、実測したら8.18kΩだったので、プログラムではその値を記入しています。
#!/usr/bin/env python
from gpiozero import MCP3002
from math import log
Vref = 3.29566
Bth=3380
Ro=10000
To=25
while 1:
pot = MCP3002(channel=0)
Volt = pot.value * Vref
Temp = -10.879 *Volt*Volt*Volt + 52.399*Volt*Volt - 118.67*Volt +132.91
Btemp = 1/(1/(To+273.15)+log( ( ((-8180*Volt)/(Volt-Vref) )/Ro) )/Bth ) -273.15
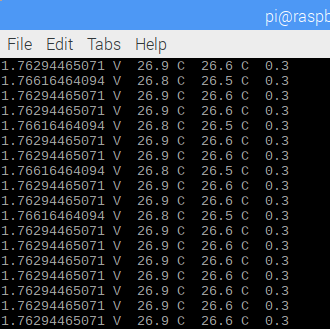
print Volt,"V ",round(Temp,1),"C ",round(Btemp,1),"C ", round((Temp-Btemp),1)
実行例です。