LTspiceのMC関数で部品のばらつきの影響を調べる(1)mc(x,y)関数、gauss(x)関数のばらつきの状態を調べる
MC関数はモンテカルロ関数とも呼ばれ、LTspiceでMC関数を用いて抵抗や容量などの素子の特性値のばらつきの影響を調べる方法をモンテカルロ解析などと呼んでいます。しかし、ここでのモンテカルロ解析はノイマンが考案した数値計算やシミュレーションで利用されるモンテカルロ法とは別物で、デバイスのばらつきの誤差解析です。
ここではまず、モンテカルロ関数の使い方や動作を調べます。ばらつき方に一様分布、正規分布の違いをLTspiceとEXCELで確認します。その後、具体的な回路で部品の精度によって出力などがどのような影響を受けるかを確認します。
●モンテカルロ法のためのmc(x,y)関数
LTspice には、モンテカルロ関数と呼ばれる素子の特性値について指定された範囲内でランダムな値を与えてくれる関数があります。この関数を利用して、素子の特性値の変動が出力にどのような影響があるか調べることができます。
mc(x,y)は、次の示す範囲内の乱数が戻される関数です。
x ×(1 - y)< 戻り値 < x ×(1 + y)
この関数で与えられる乱数は、指定された範囲内で均等にばらついた一様分布の乱数が与えられます。デバイスの特性値が指定された範囲でばらついた場合の影響を調べるのですから、指定された範囲に一様に分散された値でシミュレーションを行います。
●正規分布のためのgauss関数
ばらつきの多くは正規分布に従います。LTspiceには正規分布に従う分散をもった乱数を発生することのできる関数gauss(x)関数が用意されています。Xはσ(標準偏差)で平均値から±σの範囲内に約68.27%、±2σの範囲内に95.45%、±3σの範囲内に99.73%が含まれる釣り鐘型の分散になります。
部品のばらつきにより、期待から外れる割合などを調べる場合は、このgauss(x)関数を次のように利用します。
平均値 + gauss(x) x=標準偏差
●mc(x,y)関数、gauss(x)関数のばらつきの状態を調べる
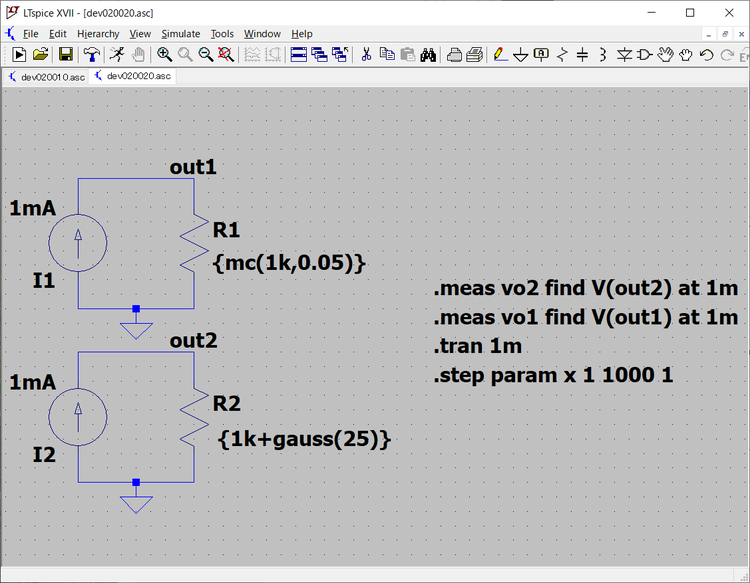
1kΩの抵抗値を、それぞれmc(x,y)関数とgauss関数でランダムの分散した値に設定し、この抵抗に定電流源から1mAの電流を流し抵抗の端子間の電圧を測定し抵抗値のばらつきを検出します。
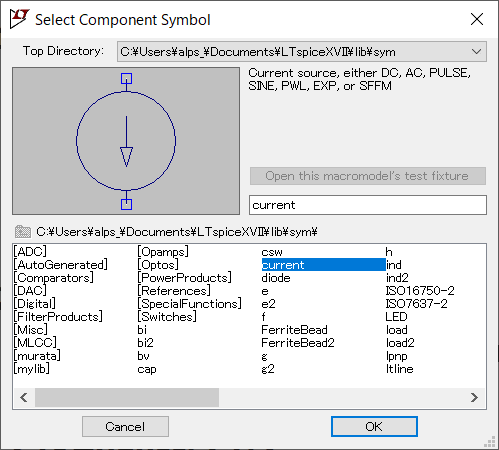
●電流源のコンポーネントcurrent
電流源のコンポーネントは、currentと呼ばれる次に示すものを利用します。電流源は、電流の流れる方向が示されています。矢印が見ているほうに接続される端子がプラス側になります。そのため、currentのコンポーネントは、設定時にCtrl+Rキーを2回繰り返し、上下反転して設定しました。
回路は電流源から1kΩの抵抗に電流を流すだけですから、電流源と抵抗、GNDだけとなります。
●mc(x,yの)関数の設定
mc(x,y)関数は、Xの値を1kΩの抵抗値を示す1k、ばらつきの範囲を示すyの値は、許容範囲を5%の抵抗を使用する場合を想定して0.05を設定します。
●gauss(x)関数の標準偏差の設定
抵抗の精度を示す許容範囲は示されています。ばらつきを示す標準偏差の値は見つかりませんでした。手許にあった茶黒赤金の5%1kΩのカーボン皮膜抵抗30本の抵抗値を、ディジタル・マルチメータで測定しました。
SANWA PC773で測定 サンプル30本 単位Ω
| 991.8 | 986.8 | 988.9 | 990.6 | 989.3 | 989.5 | 982.9 | 996.5 | 994.1 | 989.3 |
| 988.4 | 987.8 | 983.1 | 990.5 | 990.3 | 991.7 | 986.3 | 988.1 | 990.2 | 990.8 |
| 988.1 | 994.5 | 990.9 | 996.0 | 994.8 | 990.9 | 992.2 | 988.5 | 987.8 | 985.6 |
平均値=989.9 不偏分散=3.3078
989.9 + 2 × 3.3 = 996.5 > 989.9 > 989.9 - 2 × 3.3 = 983.3
989.9±6.6の範囲に95.4%の抵抗が納まる少ないバラツキのものになっています。平均値は、1kΩの表示値から10Ωずれています。このばらつきが少ないのは、同じ袋に入っていた抵抗で製造ロットが同じためと思われます。ロット内のばらつきより表示値との乖離が大きくなっています。実際の運用では、ロット間のばらつきのほうが課題となります。
gauss関数で設定するばらつきを示す標準偏差の値は、2σで5%になる値とします。したがって、
2σ = 1000Ω× 5%
σ = 25Ω
R2の設定値は、{1k+gauss(25)}とします。ばらつきを調べるために .stepコマンドでシミュレーションを1000回繰り返すことにします。
シミュレーションの結果はグラフで表示することもできますが、シミュレーションの1ms経過時の抵抗の端子間の電圧V(out1)、V(out2)を .measコマンドで測定記録します。
●シミュレーション結果
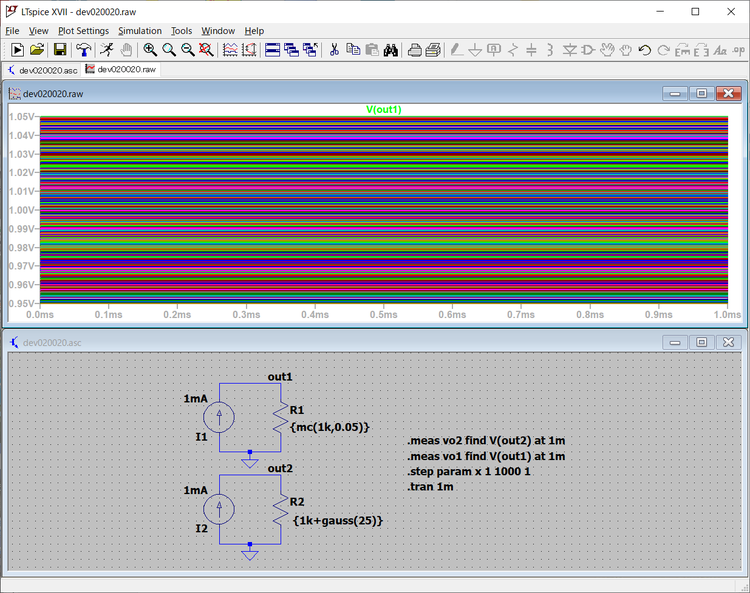
シミュレーション結果を次に示します。V(out1)の出力は、すべて1.05Vから0.95V間に収まっています。
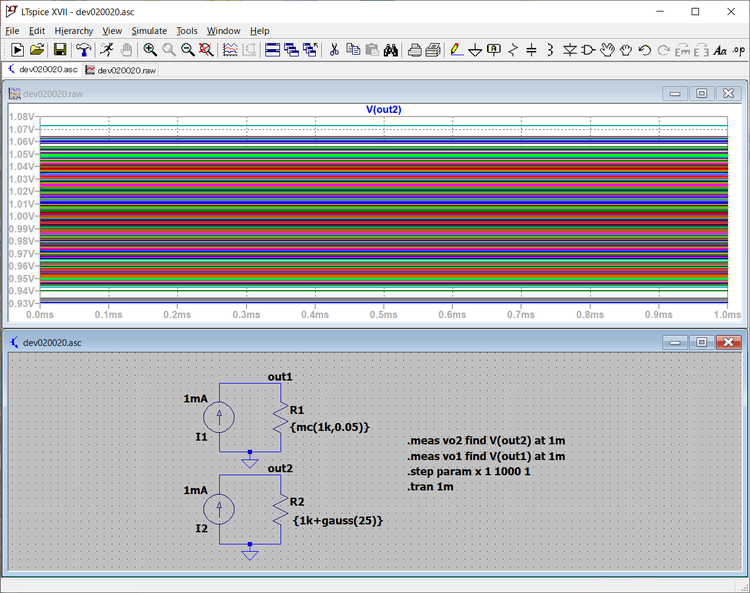
V(out2)の出力波形を次に示します。出力は、1.073Vから0.931Vの範囲にばらついています。そのばらつきの様子も、1Vの中心部では密になり、周辺になるに従い粗になっています。
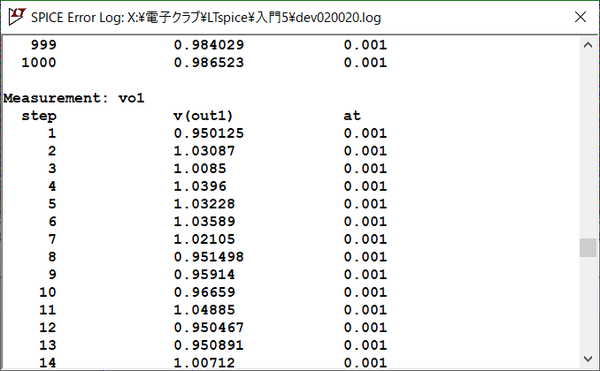
Spice Erorr logに、次に示すようにV(out1)の1msの時の値をvo1の変数に、V(out2)の1msのときの値をvo2の変数にセットした値が記録されています。このエラー・ログは、テキスト・ファイルとして回路図ファイルと同じフォルダに保存されています。vo1の値はmc()関数で1.05Vから0.95Vに均等に分布しているので、次に示すvo2のばらつきが大きいのが確認できます。
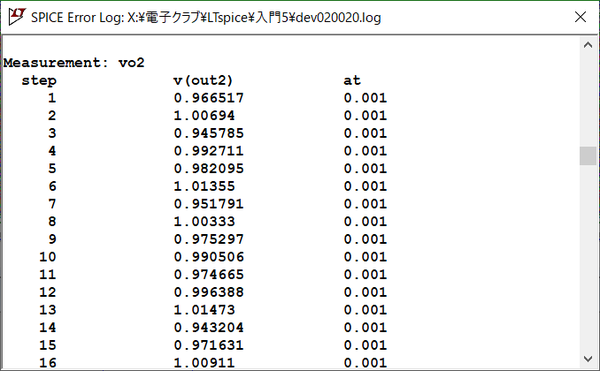
vo2はgauss関数で乱数を作成しています。このログ・ファイルはテキスト・ファイルなので、EXCELで読み込んで処理ができます。
●EXCELでログ・ファイルを読み込む
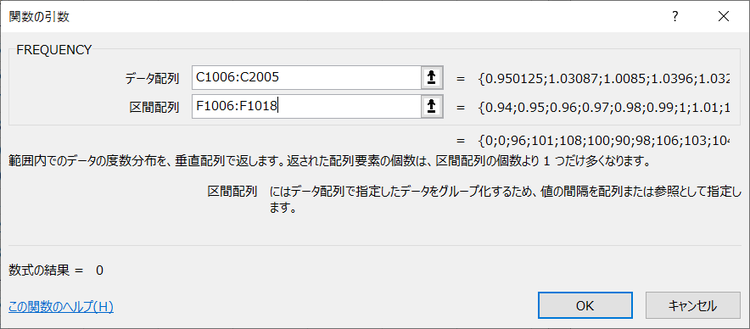
シミュレーション結果として得られたログ・ファイルをEXCELで読み込み、Frequency関数でvo1、vo2の度数分布を調べグラフ化してみます。
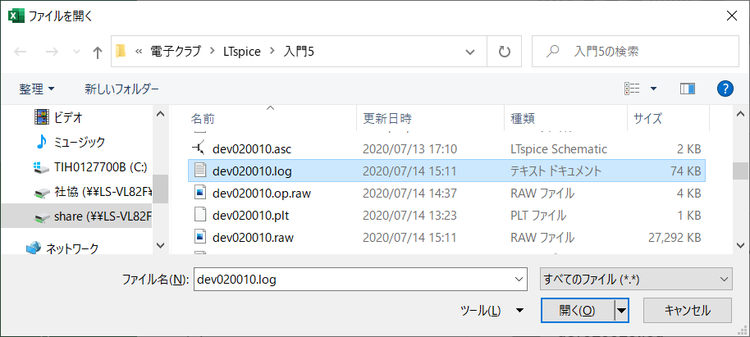
ログ・ファイルは、次に示すように回路図ファイル名にlogのエクステントのファイルとして回路図ファイルと同じフォルダに保存されます。
EXCELを起動してこのログ・ファイルを開きます。EXCELでファイルを開くとき、デフォルトではEXCELを対象としています。そのため、logエクステントのファイルは表示されません。次に示すように、表示するファイルの種類を「すべてのファイル(*.*)」に設定すると、すべてのファイルが表示されるようになります。
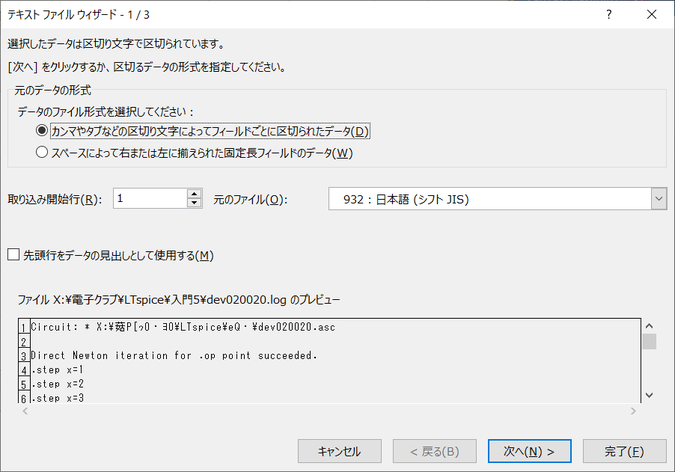
ログ・ファイルを開くと、EXCELがテキスト・ファイルを読み込むときのウィザードが表示されます。「カンマなどの区切り文字によってフィールドごとに区切られたデータ(D)」がチェックされていることを確認し、「次へ(N)」のボタンをクリックします。ログ・ファイルのフィールドがスペースで区切られています。
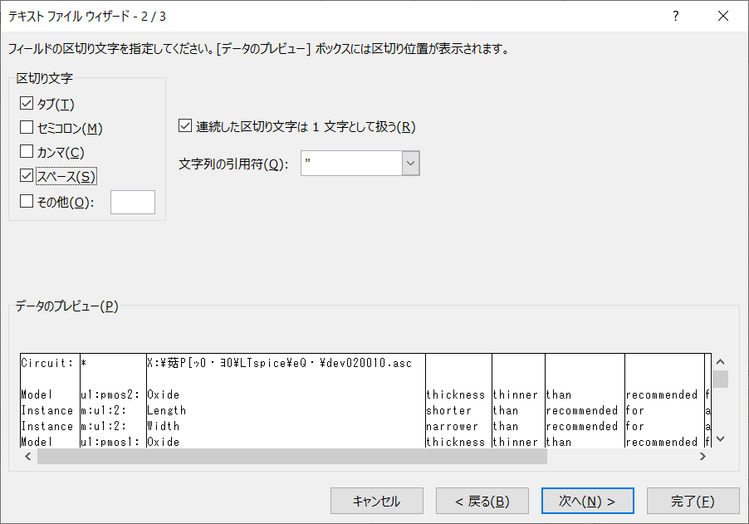
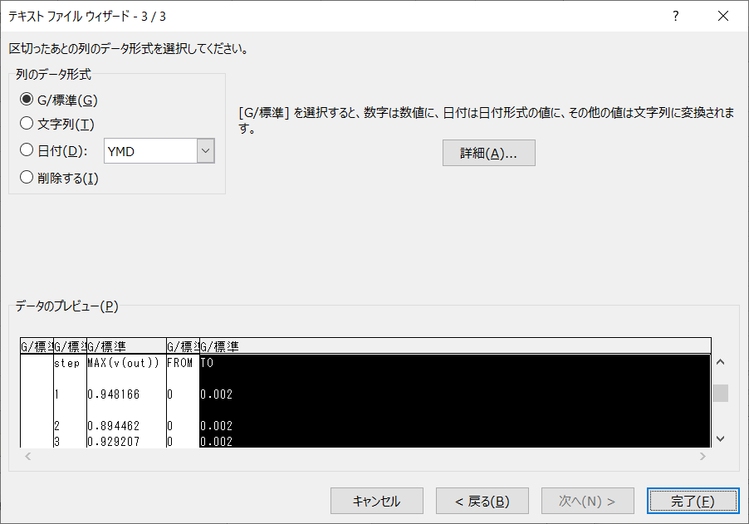
データが適切に区切られているか確認できます。確認して次に進みます。問題がある場合は戻るボタンをクリックして区切文字を確認します。Vo1、vo2のデータ以外は利用しないので、区切りの確認はしていません。
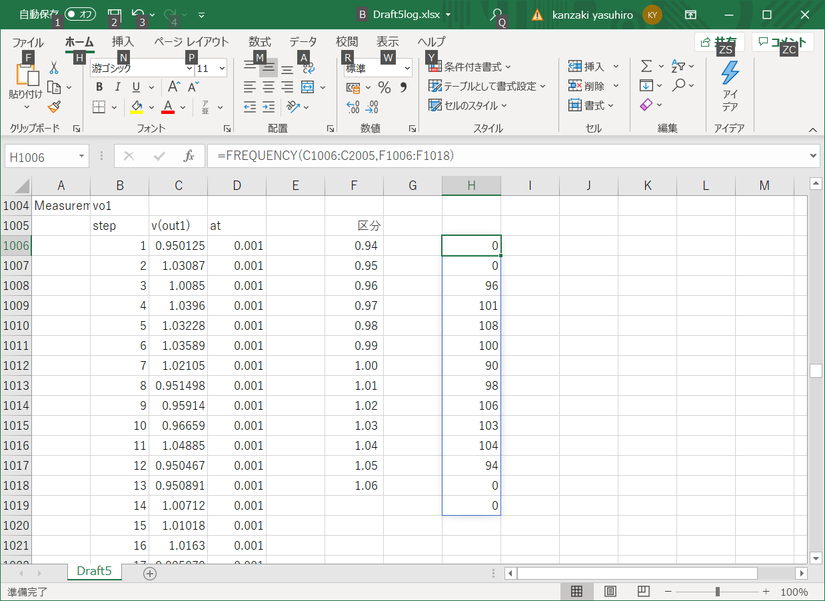
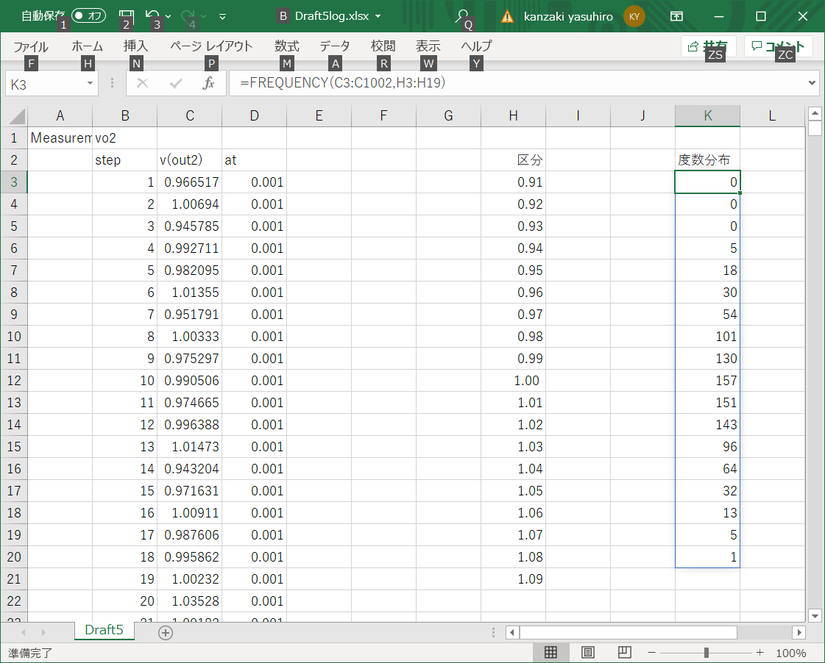
度数分布のエリアを選択し、メニューバーの挿入を選択し、おすすめグラフから棒グラフを選択します。一様分散であることが確認できます。
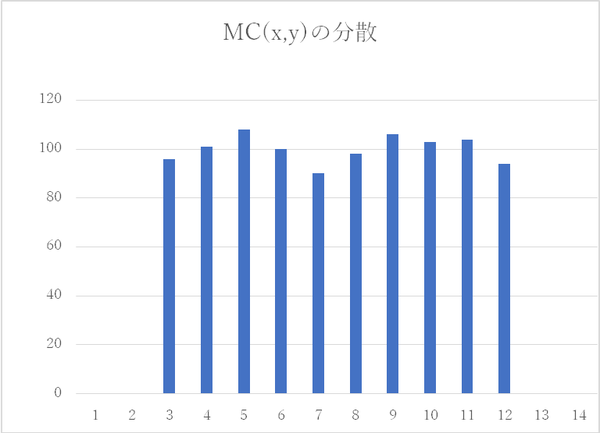
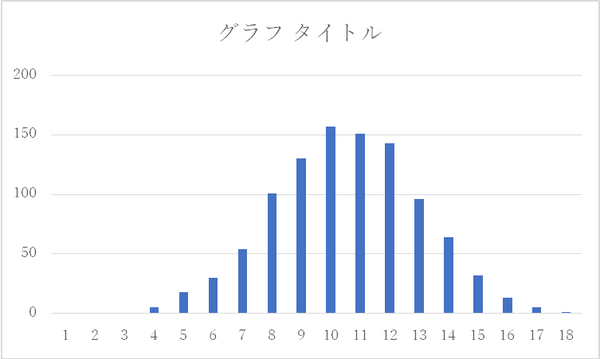
vo2のgauss関数を利用したシミュレーション結果も、同様な処理を行いグラフ化します。次に示すように、0.91から1.09までの区分としました。
グラフ化した結果を次に示します。部品のばらつきによる問題の発生割合の検討などには、こちらの方法を利用する場面が多くあります。
次回は、OPアンプによる増幅器の各素子の変動が出力にどのような影響を与えるか確認します。
(2020/7/19 V1.0)
<神崎康宏>