LTspiceのMC関数で部品のばらつきの影響を調べる(3)抵抗値のばらつきをどのように決めるか
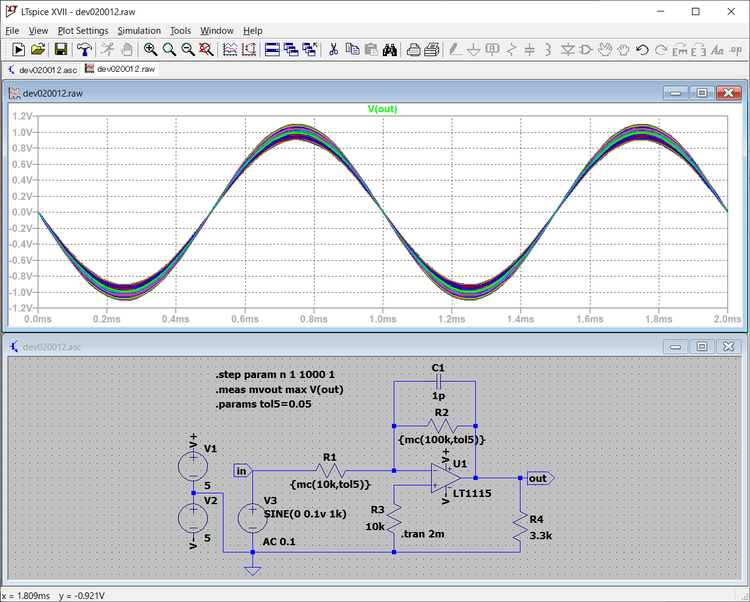
前回は、R1、R2の増幅度を決める抵抗のばらつきを、mc()関数を用いて表示値の±5%の範囲内に一様分布になるようにシミュレーションしました。
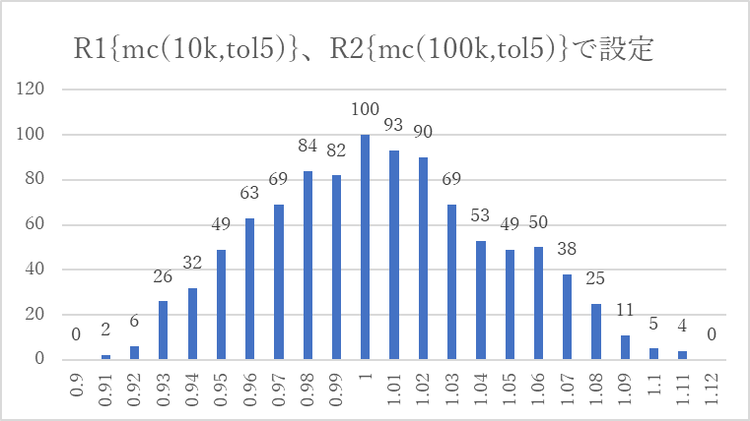
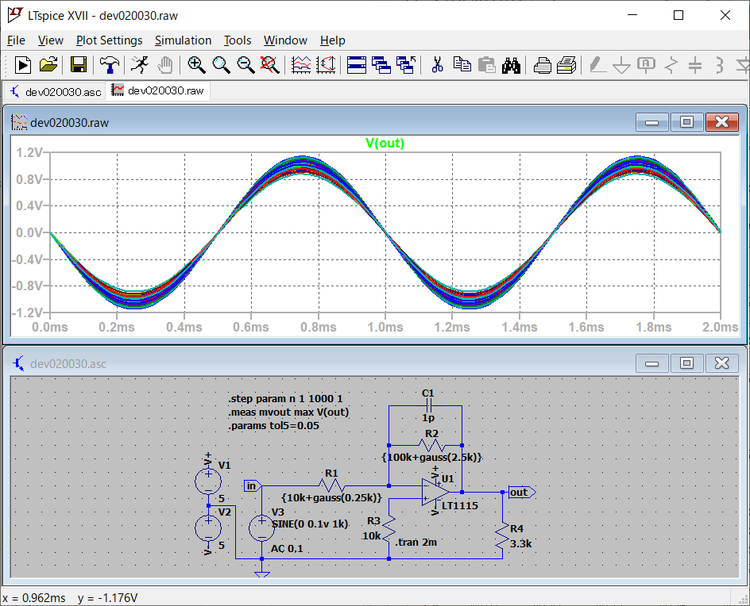
その結果、次に示すように出力のV(out)の分布は1Vをピークとして0.91Vから1.11Vの範囲に山型の分布を作っています。ばらつきを示す指数の一つに、平均値との差を二乗の総和をサンプル数-1で割った値を不偏分散があります。この不偏分散の平方根が不偏標準偏差となります。この値は0.03992Vとなっています。
母集団の特性を推定するために限られたサンプルから分散、標準偏差を推定する場合は不偏分散、不偏標準偏差と呼びます。そして不偏分散を求める場合は二乗総和を(n-1)でわります。分散を求める場合は二乗総和をnで割ります。
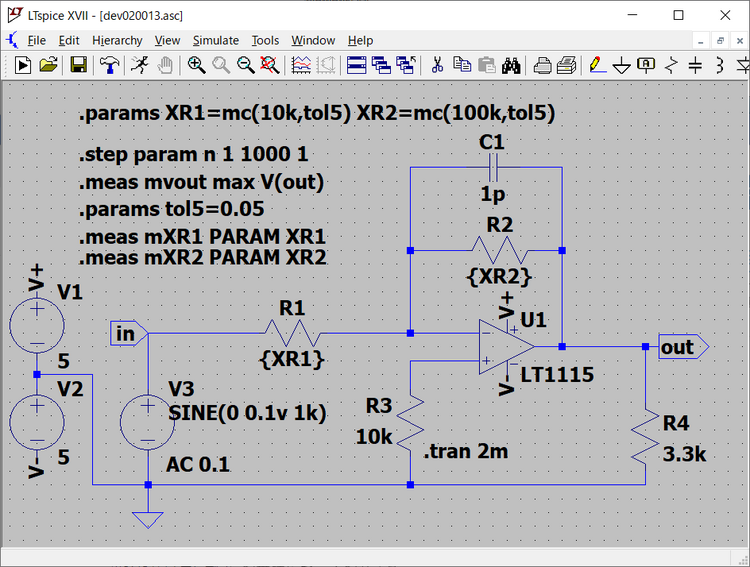
このようにばらつきの範囲が広がった様子を確認するために、各ステップごとにmc()関数で設定されたR1とR2の設定値を確認します。そのため、次に示すようにR1、R2の設定値を変数XR1、XR2として定義しその値をmc()関数でステップごとに設定します。
| .params XR1=mc(10k,tol5) XR2=mc(100k,tol5) |
各ステップごとの設定値は次に示す .measコマンドで記録します。
| .meas mXR1 PARAM XR1 .meas mXR2 PARAM XR2 |
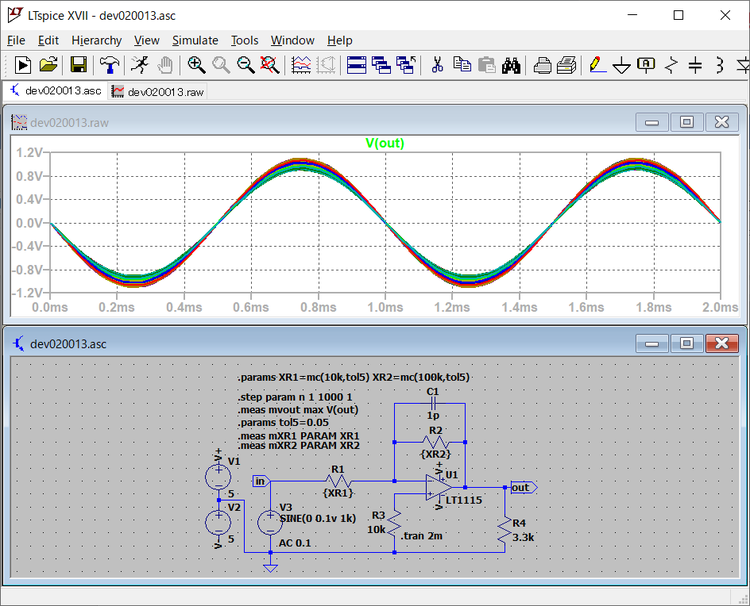
シミュレーションの結果を示します。
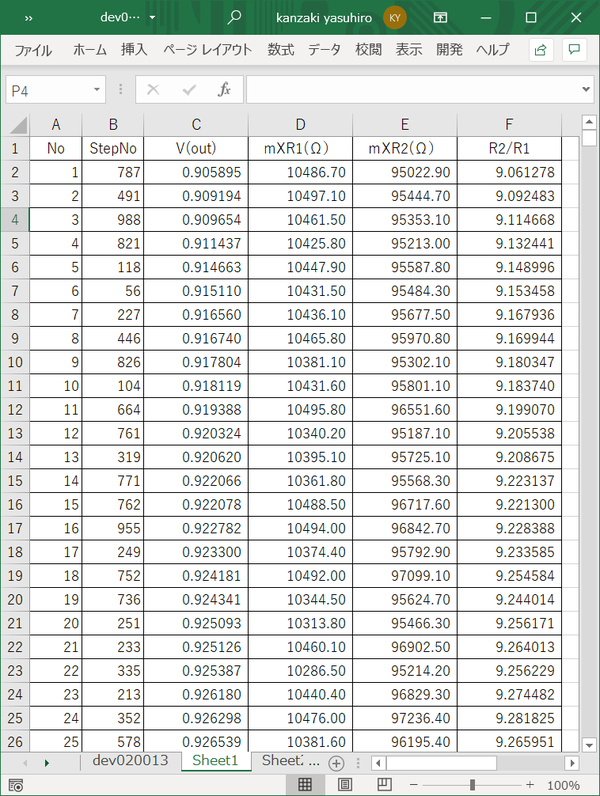
EXCELでLOGファイルを読み込みV(out)、mXR1、mXR2を並べ、次に示すようにV(out)の値が小さいものから順番に並べ替えました。No1ではmXR1=10486.70Ωは上限に近い値となり、mXR2=95022.90Ωは下限に近い値となり出力は最小値となっています。
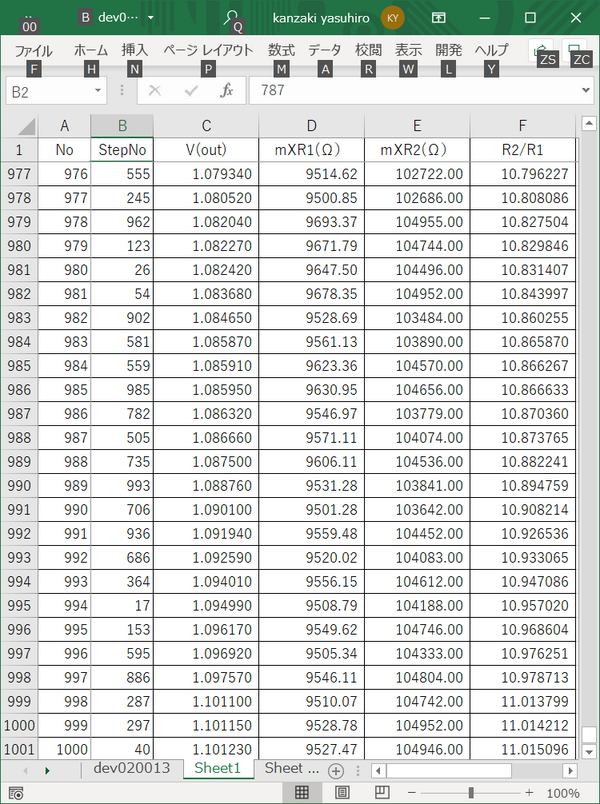
V(out)の最大値もみます。No1000のデータはmXR1が上限値近い値で、mXR2が下限値に近い値の組み合わせになっています。
●mc()関数の組み合わせで上限値、下限値の範囲がわかる
mc()関数は、範囲を区切ってその範囲内で一様分布となっています。そのため、その組み合わせとなるOPアンプの増幅率は、R1、R2の上限値/下限値を上限として下限値/上限値を下限値とする範囲に分布しています。不偏標準偏差(不偏分散の平方根)の値は0.03992Vとなっています。
●一般的なばらつきを表現するgauss関数
gauss関数では、正規分布になるような分布の値が算出されます。mc()の代わりにLTspiceに用意されているgauss関数を利用した場合の様子を示します。
|
gauss(x) x : 標準偏差(σ) |
●抵抗値のばらつきをどのように決めるか
本シリーズの1回目で手持ちのJクラス(許容度5%)カーボン皮膜抵抗30本の抵抗値をディジタル・マルチメータで実測し、そのばらつきを確認しました。
https://www.denshi.club/ltspice/2020/07/ltspicemc1mcxygaussx.html
その結果、平均値=989.9Ω 不偏標準偏差=3.3078 となりました。
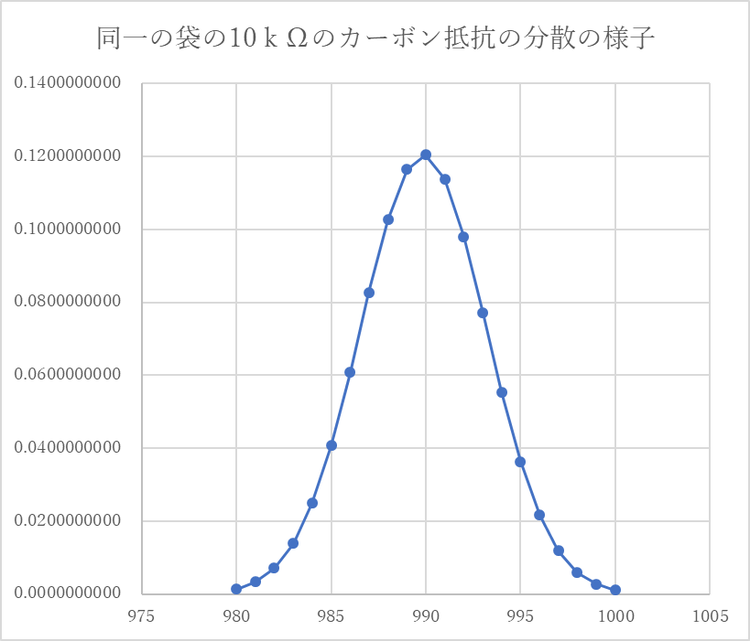
このばらつきの様子をグラフ化すると、次のようになります。これはEXCELのNORM.DIST 関数に測定値、平均値、標準偏差、関数形式を設定して各測定値ごとの確率密度関数値を得てグラフ化しました。
全体の平均が990Ω 平均値を中心に±10Ωの範囲に99.85%が含まれています。このカーボン抵抗は、表示値から10Ω(1%)少ない値を中心に、±10Ωの範囲内にほとんどの素子が含まれていることになります。抵抗値の差は、ロット内では少ないが表示値との差はロットごとに大きく異なるようです。
●gauss()関数を利用する場合には標準偏差の度合いを決める
gauss関数で設定するばらつきを、±5%の範囲内に99.9%のサンプルが含まれるように設定値を決めるとします。
このためには、標準偏差(σ)の3倍の値が設定値の5%になるようにすると、99.9%が範囲内に収まります。gauss関数で設定する標準偏差の値を決めます。
| R1は、 3σ = 10kΩ× 5% σ = 0.5/3 kΩ R2は、 3σ = 100kΩ× 5% σ = 5/3 kΩ |
●おおよそ20本に1本くらいが±5%の範囲外になる場合
正規分布の場合、平均値から±2σの範囲に95.4%のサンプルが含まれます。4.6%は範囲外となります。
| R1は、 2σ = 10kΩ× 5% σ = 0.25kΩ R2は、 |
R2の設定値は、{1k+gauss(25)}とします。ばらつきを調べるために .stepコマンドでシミュレーションを1000回繰り返すことにします。
●シミュレーションの結果
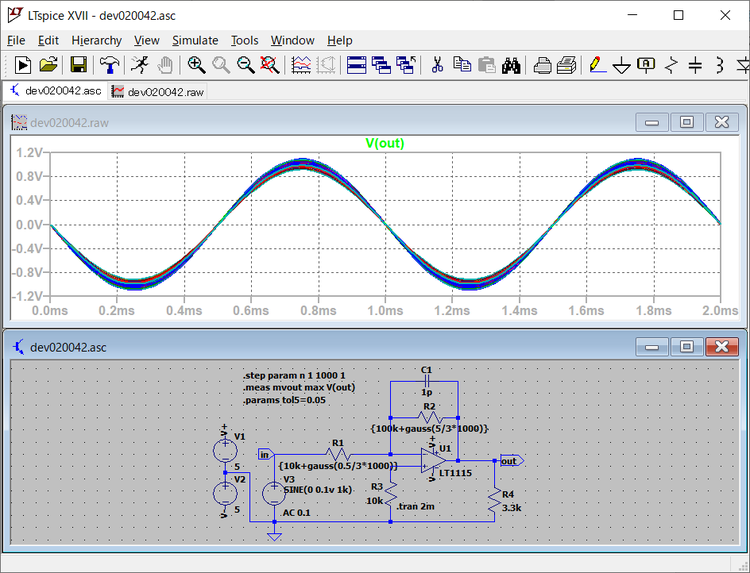
R1、R2のgauss()関数によるばらつきの大きさとV(out)の変動の様子を次に示します。
抵抗値の許容差を5%としてガウス関数で設定する標準偏差を2σと3σの場合と、R1のみ変動したときとR1、R2をともに変動させたときの状況です。
| 5%以内の割合 | 99.9% | 99.9% | 95.4% | 95.4% |
|---|---|---|---|---|
| R1の標準偏差 | 0.5/3kΩ | 0.5/3kΩ | 0.25kΩ | 0.25kΩ |
| R2の標準偏差 | 0 | 5/3kΩ | 0 | 2.5kΩ |
| V(out)の不遍標準偏差 | 0.01659V | 0.02286V | 0.02469V | 0.02469V |
R1、R2をともにmc()関数でシミュレーションしたV(out)の不遍標準偏差が0.03992Vとなっていました。その値より小さなばらつきになっています。
mc()関数では、部品のばらつきによる下限値、上限値を確認するのに便利です。多くの場合部品のばらつきは平均値を中心にばらつくので、部品のばらつきによる結果のばらつきの様子を確認するのに便利です。
(2020/9/15 V1.0)
<神崎康宏>