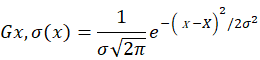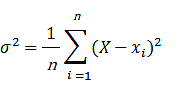LTspiceのMC関数で部品のばらつきの影響を調べる(4)抵抗値のばらつきを短時間で確認する
前回までのばらつきの確認は、抵抗値のばらつきでOPアンプの増幅度がどのように変化するかを確認しました。OPアンプの増幅度を規定するフィードバック回路の抵抗値が、増幅度の変動に基づいた計算式通りの変動となりました。
毎回過渡解析で出力信号の大きさをシミュレーションして確認しました。2msのシミュレーション期間ですが、1000ステップの繰り返しを行っているので2700秒とかなりの時間がかかります。
●抵抗値のばらつきの確認だけなら
抵抗値のばらつきの確認だけなら、定電圧源を接続して抵抗に流れる電流値を測定するか、定電流源を接続し抵抗の端子間の電圧を測定することで実現できます。測定も回路の直流バイアスの設定が終われば完了するので .op のシミュレーション・コマンドでシミュレーションを行います。
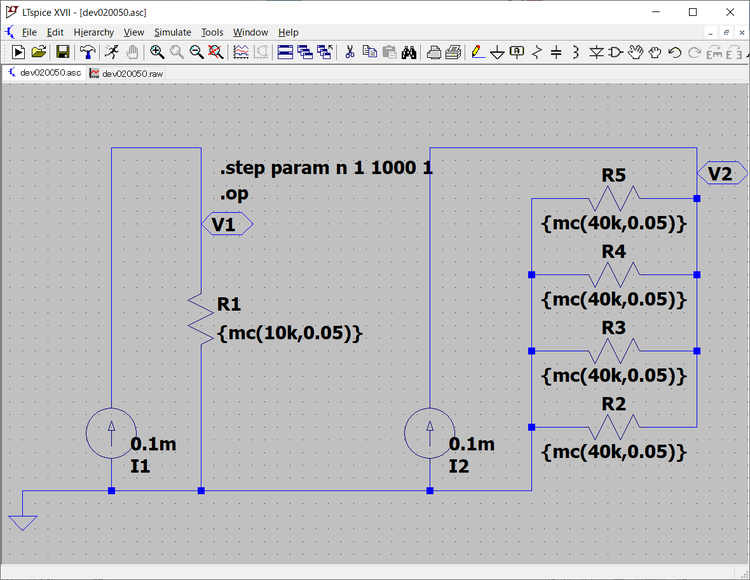
回路図は次のようになります。
R1は10kΩでmc(10k,0.05)関数で5%(0.05)の均一な変動を行うように設定しました。mc()関数は第2の引数で示された範囲で偏りのない均等なばらつきもった値が戻されます。この抵抗に0.1mAの定電流をI1の定電流源から供給し、V1のポイントの電圧を測定しR1の抵抗値の変動とみなします。10kΩ×0.1mAで1Vの出力、5%の変動で0.05Vの電圧になることが期待されます。
同様にI2の定電流源から0.1mAの定電流を、4本の平行に接続したR2からR5の40kΩの抵抗に流し、V2の電圧を測定してmc(40k,0.05)で、それぞればらつきのある4本の抵抗が合成されたのち、ばらつきがどのように変化するかを確認します。
.step コマンドでシミュレーションを1000回繰り返します。
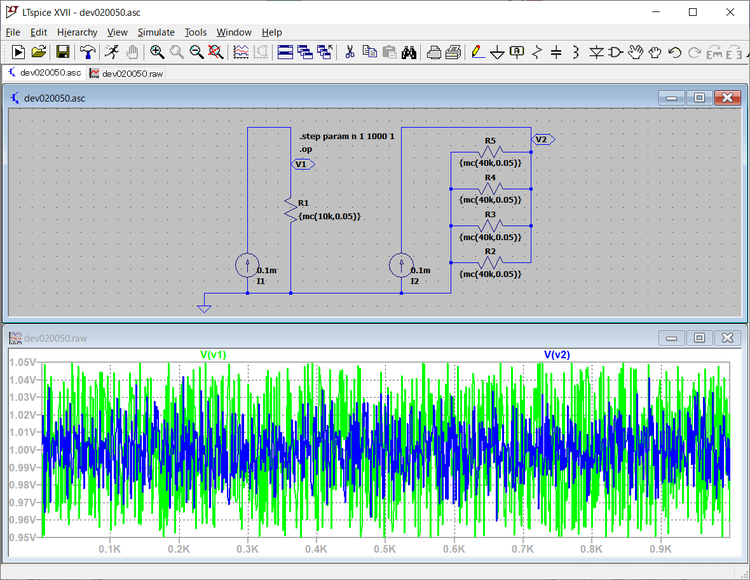
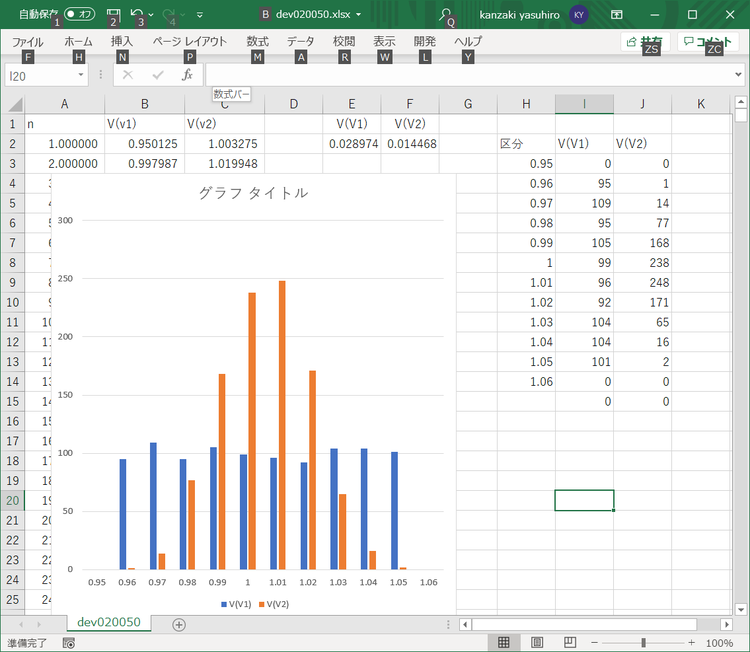
シミュレーションの経過時間は、Spice Error LogにTotal elapsed time として記録されているので、確認できます。27秒でした。V1とV2の電圧をグラフ画面に表示すると、次に示すように、横軸が0.1K刻みでフルスケール1Kのステップの回数、縦軸が電圧を示すグラフに、V(V1)が緑色、V(V2)が青色の線で表示されました。
V(V1)の緑のラインは0.95Vから1.05Vの間にばらついていますが、V(V2)の青のラインはばらつきの範囲が少なくなっているのがグラフからもよくわかります。
●ばらつきを定量化する
ばらつきの状態をみるために、シミュレーション結果をテキスト・ファイルに書き出し、EXCELを使ってばらつきを確認してみます。
●テキストフ・ァイルの作成
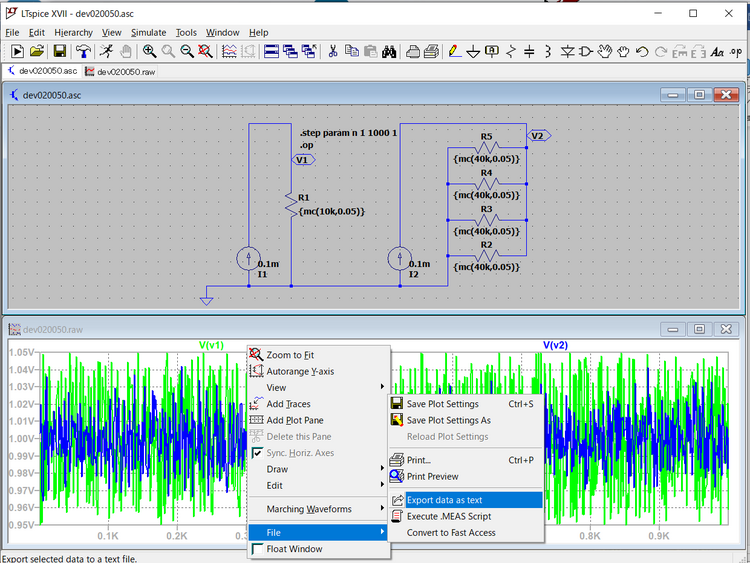
シミュレーション結果をテキスト・ファイルにエクスポートするためには、グラフ画面をマウスの右ボタンでクリックし、次に示すようなドロップダウン・リストを表示します。
リストから、
File > Export data as text
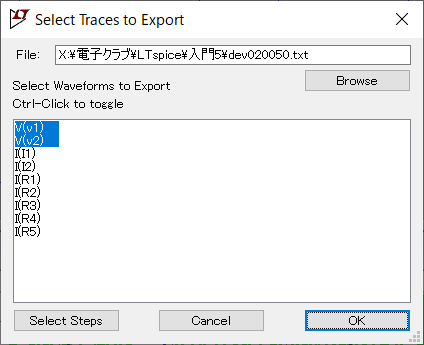
を選択すると、ファイル名が回路図のファイル名と同じでエクステントがtxtのファイルを出力するためのガイダンスが、次のように表示されます。
グラフに表示されているV(V1)、V(V2)が選択されています。この選択されている項目の値がテキスト・データとしてエクスポートされます。
マウスでクリックして、任意の項目をここで選択することもできます。複数の項目を選択する場合はCtrlキーを押しながらマウスでクリックします。
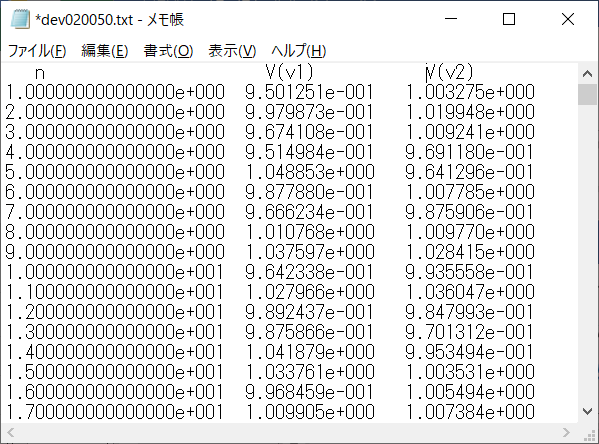
エクスポートされたファイルを、メモ帳で確認した様子を次に示します。最初の1行が見出しで1000行のデータが続きます。ステップ数、共に1V前後のV(V1)、V(V2)のデータが並んでいます。
●正規分布
いろいろな測定結果、統計調査の結果は、取り除くことのできない多数の原因でばらつきます。このばらつき(分布)は多くの場合、正規分布に従います。その正規分布は次に示す「分布の中心」と「分布の幅」で表現できます。
X=分布の中心 = 真の値=何回も繰り返し十分な回数測定した平均値
σ=分布の幅 = 何回も繰り返し十分な回数測定したときの標準偏差 σ で表す
連続変数 xに対する正規分布(ガウス分布)は、次の式で求められます。
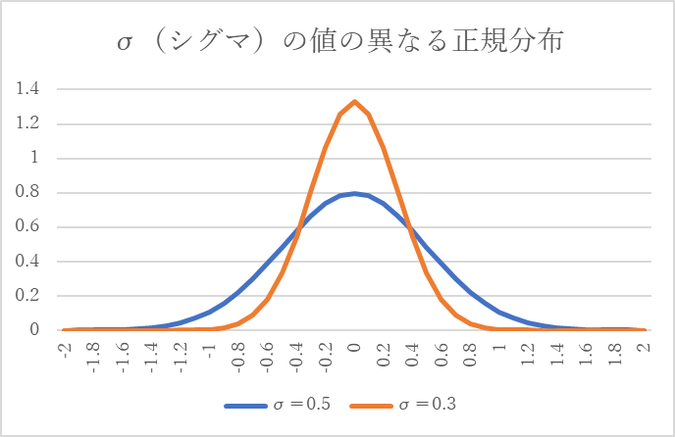
X、σを与えてこの式を計算する関数が、EXCELに用意されています。Norm.dist()関数です。平均0、σが0.5と0.3と異なった正規分布の計算を行い、グラフ化したものを次に示します。
σの値が小さいと、ばらつきの幅が小さくなっています。±1σの間に68.2%が含まれるばらつきとなります。
●分散
ばらつきを分散で表します。この分散は、真の値とサンプルの測定値との差の二乗の和をサンプルの数nで割ったもので、σの二乗になり次の式で与えられます。
(X:真の値 x:サンプルの値 n: サンプルの数)
●不偏分散
分散は母集団のばらつきを示すもので、実際は母集団からサンプルを取り出し測定することになり、母集団のばらつきを推定するものになります。その場合、次に示す式で表し「不偏分散」と呼びます。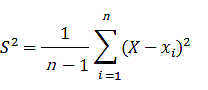
この場合のSを標本標準偏差と呼ぶことがあります。この標本標準偏差S(不偏分散のプラスの平方根)は、母集団の標準偏差の不偏推定値とはなりません。少し補正が必要です。
●このファイルをEXCELで読み込む
EXCELを起動して、エクスポートしたテキスト・ファイルを開きます。見出しのステップ数のn、V(V1)、V(V2)に続いて2行目から1001行目までデータが読み込まれます。
●ばらつきを求めるためEXCELで標準偏差を求める
ここで、平均値、標準偏差、不偏標準偏差、分散、不偏分散をEXCELで求め、併せてばらつきの様子をグラフ化してみます。
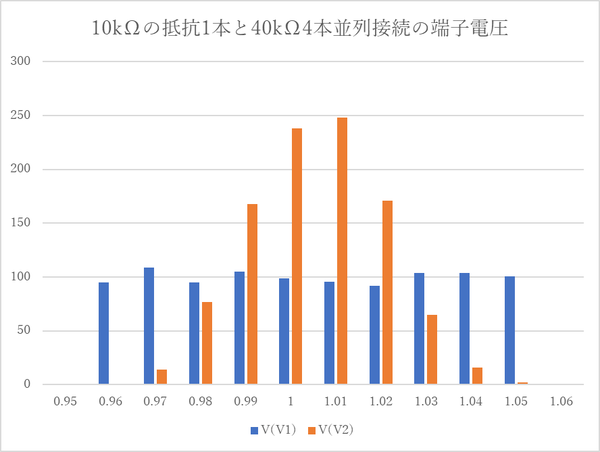
V(V1) : 許容差5%10kΩの抵抗の端子電圧
V(V2) : 許容差5%400kΩの抵抗4本を平行接続した端子電圧
これらの抵抗値は、mc()関数で一様分布の変動を1000回与え、シミュレーション結果をグラフ表示します。
縦軸は、各端子の電圧の範囲となったサンプルの頻度です。青色のグラフはV(V1)でばらつきが一様分布なので、0.95Vから1.05Vの範囲に均等に分布しています。橙色は4本の抵抗の平均値となるので、ばらつきの範囲が狭くなるのと合わせて山形の分布になっています。
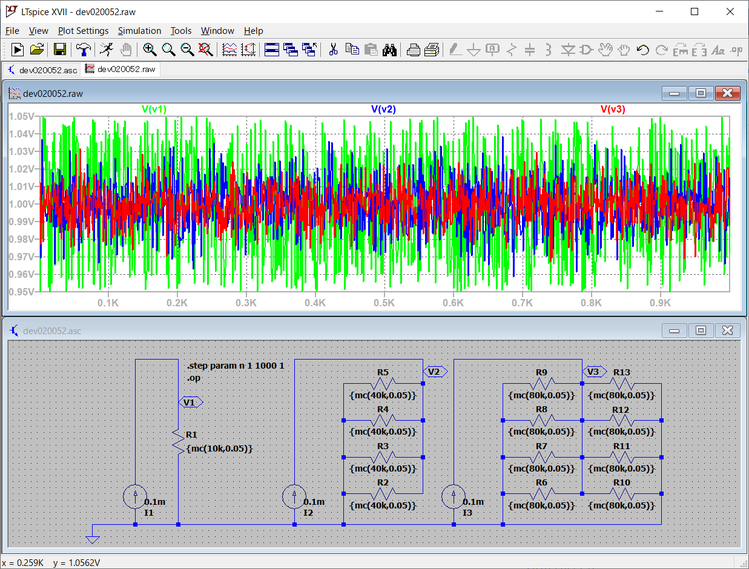
次に80kΩの抵抗を、8本並列に接続した次の回路でシミュレーションしました。
8本を並列に接続した回路は、よりばらつきが小さくなっています。
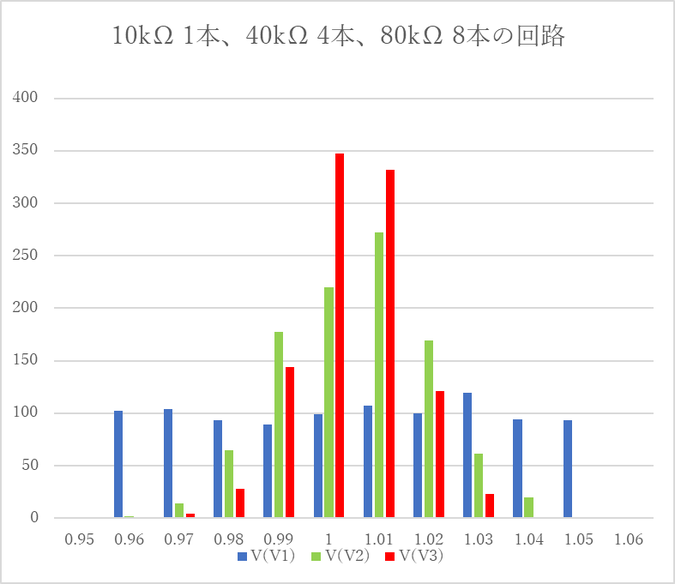
この様子をテキスト・ファイルとしてエクスポートして、EXCELでばらつきを確認します。
4本の並列接続より8本の並列接続のほうがよりばらつきが小さくなり、中心の頻度が大きな値となっています。
EXCELのVER.S関数で不偏分散を、STDEV.S関数で標本標準偏差を計算し、まとめました。
| V(V1)n=1 | V(V2)n=4 | V(V3)n=8 | |
| 不偏分散 | 8.420E-04 | 2.030E-04 | 1.045E-04 |
|---|---|---|---|
| 標本標準偏差 | 2.902E-02 | 1.425E-02 | 1.022E-02 |
V1は抵抗1本のばらつき、V2は抵抗4本を合成し平均化したもののばらつき、V3は抵抗8本の平均化したもののばらつきとなります。nの数を増大するに従いばらつきは小さくなります。
不偏分散は平均値を求めるサンプル数nの値に反比例します。n=4のときはn=1のときの1/4、n=8のときはn=1のときの1/8になっています。標本標準偏差は平均化するサンプル数nに関して 1/√n になります。
測定を繰り返して平均値を求めると、測定精度が上がる場合の仕組みも同様なものです。
(2020/10/5 V1.0)
<神崎康宏>